Graphs are a powerful way to represent and analyze relationships between various entities In C++, a graph is a data structure that consists of a finite set of nodes (vertices) and a collection of edges connecting these nodes.

Let's understand through an example:

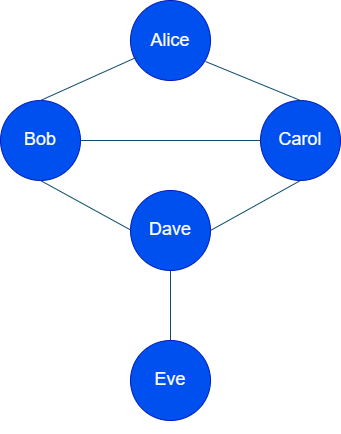
Suppose we have the following individuals:

1. Alice
2. Bob
3. Carol
4. Dave
5. Eve

And the connections (friendships) between them are as follows:

• Alice is friends with Bob and Carol.
• Bob is friends with Alice and Dave.
• Carol is friends with Alice and Eve.
• Dave is friends with Bob.
• Eve is friends with Carol.

We create a graph representing the connections between the individuals-

Some key terms about graphs:

1. Nodes (Vertices): These are the individual elements of the graph, representing entities or points. Each node can have a label or a value associated with it.
2. Edges: Edges are connections between nodes, indicating a relationship or a link between the connected nodes. Edges can be directed (pointing from one node to another) or undirected (bidirectional).

Vertices (Nodes):

V={Alice, Bob, Carol, Dave, Eve}

Edges (Connections):

E={(Alice, Bob), (Alice, Carol),(Bob, Dave), (Carol, Eve)}

Graph Terminologies

1. Adjacent: Two vertices are adjacent if they are connected by an edge. For example, Alice and Bob are adjacent because they are connected by the edge representing their friendship.
2. Degree of a Vertex: The degree of a vertex is the number of edges incident to it. For instance, Alice has a degree of 2 because she is friends with Bob and Carol.
3. Directed Edge: An edge with a specific direction, indicating a one-way connection from one vertex to another.
4. Undirected Edge: An edge without a specific direction, representing a bidirectional connection. If Alice is friends with Bob, it implies that Bob is also friends with Alice. The above graph is an undirected edge graph.
5. Path: A sequence of vertices where each adjacent pair is connected by an edge. For example, the path "Alice -> Bob -> Dave" represents a sequence of friendships that connect these individuals.
6. Cycle: A path where the first and last vertices are the same, forming a closed loop. For instance, if Alice is friends with Bob, Bob is friends with Dave, and Dave is friends with Alice, you have a cycle "Alice -> Bob -> Dave -> Alice.”
7. Connected Graph: A graph where there is a path between every pair of vertices. The above graph is connected because there is a path between every pair of vertices (individuals).
8. Disconnected Graph: A graph with one or more components where some vertices cannot be reached from other vertices.
9. Cyclic Graph: A graph that contains at least one cycle. (Alice, Bob, Carol ), (Alice, Bob, Dave, Carol ) and (Bob, Carol , Dave) forms a cycle.
10. Acyclic Graph: A graph that does not contain any cycles.

Graph Representation

There are two common ways to represent graphs.

1. Adjacency Matrix:

An adjacency matrix is a 2D array where each row and column represent a vertex, and the value in cell (i, j) indicates whether there is an edge between vertex i and vertex j. For weighted graphs, the cell value could represent the weight of the edge.

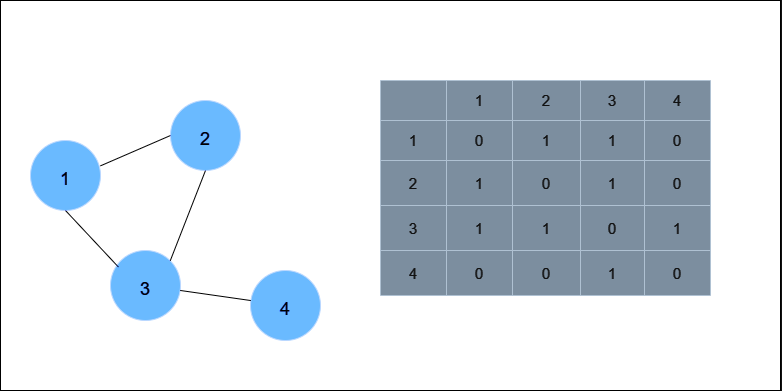
• The rows and columns represent the vertices (numbers).
• The entry at row i and column j (cell i, j) indicates whether there is an edge between vertex i and vertex j. If there is an edge, the value is 1; otherwise, it's 0.

For example:

• Cell (1, 2) and cell (2, 1) both have a value of 1, indicating an edge between vertex 1 and vertex 2.
• Cell (3, 4) and cell (4, 3) both have a value of 1, indicating an edge between vertex 3 and vertex 4.

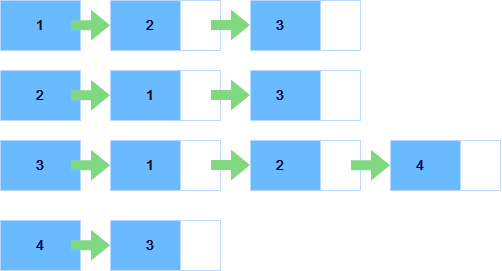
  2. Adjacency List:

An adjacency list represents each vertex as a list of its neighbors. It can be implemented using an array of lists or a hash map where each vertex maps to a list of its neighbors. Below an adjacent matrix has been shown:

Uses of Graphs:

• Social Networks: Modeling connections between individuals in social networks.
• Transportation Networks: Representing roads, highways, and flight routes for route planning.
• Computer Networks: Modeling connections between computers and network devices.
• Recommendation Systems: Analyzing user preferences and connections for recommending products or content.
• Dependency Resolution: Solving problems involving dependencies between tasks or components.
• Circuit Design: Analyzing connections in electronic circuits.
• Data Structures: Used as a foundation for various algorithms and data structures, such as shortest path algorithms (Dijkstra's, Bellman-Ford), searching algorithms (DFS, BFS), and more.